Investment Returns – How to Calculate Return

First, we saw how we could use holding period return to calculate the return of a simple investment with two cash flows, one at the beginning and the other at the end of the period. Next, I introduced the concepts of time-weighted return (“TWR”) and money-weighted return (“MWR”), the two preferred methods used by investment professionals to calculate return.

Here I’ll delve deeper into investment returns, showing how both TWR and MWR are calculated. I will use a real world example to show how these two performance measures can differ, sometimes substantially.

Let’s return to my friend Tim. He asked me how to calculate his fund’s “actual performance.” Using DFEOX as an example, we’ll compute the fund’s 2015 TWR. Then we’ll calculate Tim’s 2015 MWR based on his actual contributions.

Calculating Time-Weighted Return

TWR illustrates the hypothetical growth of $1 invested over some time period. To calculate annual TWR, we measure how much $1 would grow if invested on January 1^st and withdrawn on December 31^st of the same year.

The calculation is fairly straightforward. First, calculate the holding period return for each market day of the year. Second, compound each holding period to arrive at the end-of-period TWR. Let’s return to my friend and calculate DFEOX’s 2015 TWR.

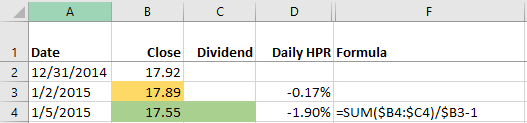
The first thing we need is a list of DFEOX’s daily prices as well as dividend payments. I used Yahoo, where I found daily prices for DFEOX 2015 here and dividends here. (We include dividends because excluding them would underestimate total return).

With this data, we can calculate DFEOX’s daily holding period return for every market day in 2015. I used the holding period return formula:

HPR = (ending value / beginning value) – 1

So “Daily HPR” is simply the end of the day price (B4) plus any dividends (C4), if applicable, divided by the previous day’s closing price (B3). For example, the HPR for January 2^nd is -.17% because $17.89 is .17% less than $17.92, the price on December 31^st. (In case you’re wondering what happened to January 1^st, the stock market was closed that day).  If we do this 252 times, we get the HPR for each market day in 2015. Although I can’t show all 252 calculations here, I’ve made my spreadsheet available online. (You can download a copy by clicking File > Download as).

Next, calculate the compound return. This is the trailing return of the hypothetical $1 that Tim deposited on December 31^st. To find compound return, we have to use multiplication, which takes into account compound interest.  For example, to calculate the compound return through January 5^th:

Compound return = (1 + HPR_{January 2nd}) x (1 + HPR_{January 5th}) – 1 = (1 + -0.17%) x (1 + -1.90%) -1 = -2.06%

Tim’s initial dollar is now worth -2.06% less, or $0.9794. To get the year-end return, we need to compound all of the 252 holding period returns in 2015.

If we compound returns for every day of the year, we get an annual compound return of -1.35%. This means that $1 invested at the beginning of the year is worth $0.9865 at year end. To check our math, we can compare our result with the fund’s 2015 annual return reported by Morningstar. Spoiler alert – Morningstar reports… -1.35%.

So arithmetic works! Now let’s turn our attention to calculating Tim’s MWR, which will tell us how his actual contributions affected his return.

Calculating Money-Weighted Return

Unlike in time-weighted return, in money-weighted return the timing and size of cash flows matter. Money is “weighted” in the sense that, one, larger deposits (withdrawals) count more toward return than smaller ones and, two, equal-size deposits (withdrawals) made at the beginning of a period count more than those made at the end. For example, $1,000 invested on January 1^st will count more toward annual MWR than $1,000 invested 11 months later on December 1^st.

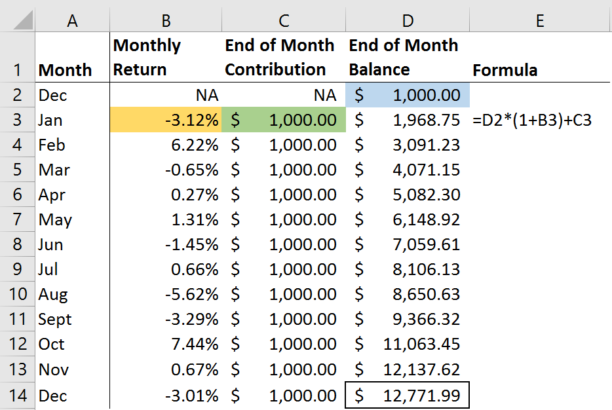
So how do we calculate MWR? First, we need to know our beginning and ending balances as well as all contributions and withdrawals in between. With this information, we can calculate the internal rate of return, or simply “IRR,” that gets us from the beginning to the end of the period.

Returning to Tim, he began with $1,000 in his account.  At the end of January, Tim’s original balance grew by -3.12%. He also added another $1,000, leaving him with $1,968.75 in his account.

If we keep doing this for eleven months, we see that at the end of 2015 Tim has $12,771.99 in his account. Again, I’ve made my full calculations available online for you to view or download.

Next, we need to figure out what rate of return Tim would need so that his account at year end is worth $12,771.99, taking into account all of his contributions. This calculation can be rather complicated to do by hand. Luckily, spreadsheet programs like Excel can calculate IRR rather easily given dates and cash flows.

Plugging the numbers into the XIRR function in Excel, we calculate Tim’s 2015 MWR as -3.47%. Tim’s timing was unfortunate. Had he put all of his money into DFEOX on January 1^st, his return would have been about 2% higher. But some years you win, some you lose. Importantly, after all this math, Tim finally knows how to calculate his “actual performance.”

In Conclusion

If you’ve made it this far, you should have a good understanding of how to calculate investment returns. Time-weighted return tells us how a hypothetical $1 would grow over some time period. It’s most useful for comparing how your fund performed relative to some other fund or benchmark. Money-weighted return tells us your realized return, given actual contributions and withdrawals. Although it’s not useful for comparison purposes, it does tell you how the timing of your additions and subtractions affected your end result.